Линевич
Э. И.
АНАЛИТИЧЕСКИЙ
ВЫВОД ФИЗИЧЕСКИХ КОНСТАНТ НА ОСНОВЕ КЛАССИЧЕСКИХ ПРЕДСТАВЛЕНИЙ
Ключевые
слова: гравитация, геоцентрическая постоянная, постоянная Планка, заряд,
электрон, напряженность.
Получены аналитические выражения для основных физических констант. Сделан
вывод о непостоянстве кавендишевой гравитационной постоянной и возможности
гравитационного взаимоотталкивания тел.
Центрические
постоянные, используемые в астрофизических расчетах, как известно, имеют
две формы записи. Например, геоцентрическая постоянная
,
(1)
, (2)
где 
– кавендишева гравитационная
постоянная, М - масса Земли, V
- потенциал соответствующей гравитационной поверхности, R - расстояние
от этой поверхности до центра Земли.
Для специалистов чрезвычайно важно знать, действительно ли является универсальной постоянной. Окончательного ответа на этот вопрос, начиная с Ньютона и по настоящее время, не существует. В предлагаемом материале автор выносит на суд читателя свой вариант решения и его результат.
В работе все формулы даются в Международной системе единиц (СИ). В соотношение
(1) входит, как коэффициент,
полученный в лабораторных условиях, который затем переносят на астрономический
масштаб, предполагая, что он при этом остается неизменным. Проверку его
осуществляют по наблюдаемому движению космических тел, сравнивая с их
центрическими постоянными по формуле (2). Если рассматривать земной шар,
как абстрактный геометрический объект, то формулы (1) и (2) описывают
одно из его внешних свойств, при этом исследователь, находящийся внутри
объекта, представляет это свойство формулой (1), а исследователь, находящийся
снаружи объекта – формулой (2). При сравнении (1) и (2) на достоверность
вычисляемой по ним геоцентрической постоянной, более предпочтительной
является формула (2).
Рассмотрим подробнее физический смысл входящих в нее параметров. Представим
круговое вращение точки по радиусу R. Оно является геометрическим
сложением ее двух линейных движений в ортогональных направлениях. Используя
эти направления, как оси X и Y, отложим на них пройденные
точкой расстояния (см. рис. 1). Пусть скорость V постоянна и,
для примера, равна 1,5 м/сек. Будем отмечать пройденный путь через интервалы
времени t кратными одной секунде. На рис.1 показаны расстояния
через 1,2 и 3 секунды. В результате у нас получились прямоугольники, площади
которых 
,
и 
увеличивались
равноускоренно, в соответствии с формулой 
, (3). В данном
случае роль ускорения выполняет квадрат скорости.
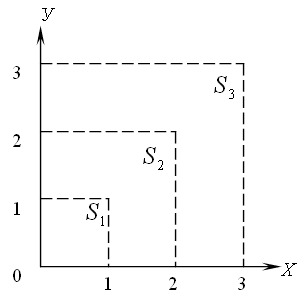Рис.1.
Движение точки с постоянной скоростью
одновременно в двух ортогональных направлениях.
В более общем случае:
,
(4)
где 
и 
–
ортогональные составляющие скорости движения.
Таким
образом, мы можем утверждать, что потенциал 
гравитационной поверхности показывает скорость изменения её площади (является
квадратным ускорением).
В
литературе, посвященной ОТО (Общая теория относительности), такую поверхность,
с целью наглядности, иногда показывают в виде раздувающегося шара. В реальности
это неверно. Площадь шара равна 
,
а площадь гравитационной поверхности (g – поверхности), согласно
соотношению (3), равна 
.
Скорость изменения объёма, ограничиваемого этой поверхностью, равна центрической
постоянной гравитирующего объекта (иначе, её можно назвать кубическим
ускорением), поэтому формулы (1) и (2) можно переписать таким образом
,
(5)
где Т – время одного оборота со скоростью V по g
– поверхности.
Из последнего соотношения, как следствия, вытекают законы Кеплера и закон всемирного тяготения Ньютона. Отсюда можно сказать, что свойства центрической постоянной являются фундаментальной основой законов небесной механики.
Следует заметить, что для физического тела первой g – поверхностью
является поверхность изменения направления градиента гравитации (ПИНГГ).
Для земного шара она не совпадает с его твердой границей (см. рис. 2),
главным образом из-за наличия атмосферы, поэтому радиусом Земли для внешнего
наблюдателя является радиус ее ПИНГГа.
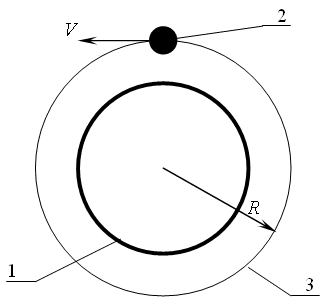
Рис.2. Круговое движение тела массой m с первой космической скоростью
(7,9 км/сек) вокруг Земли: 1 – земной шар, 2 – тело, 3 – поверхность изменения
направления градиента гравитации (ПИНГГ), R – её радиус.
В дальнейшем, нам понадобится аналитическое соотношение
для постоянной Планка. Для его вывода воспользуемся схемой на рис. 2.
Потенциальная энергия тела 2 равна 
,
умножим W на период Т вращения и найдем его значение
,
(6)
Полученное
выражение, применительно к атому водорода, дает значение постоянной Планка
,
(7)
где 
– масса электрона, 
– скорость на первой боровской орбите, 
– ее радиус.
Физический смысл формулы (7), с учетом рис. 2, в том, что она показывает
произведение энергии (которую необходимо затратить для выноса массы электрона
на первую g - поверхность атома водорода) на период оборота по
этой поверхности. Скорость электрона на боровской сфере, в некотором смысле,
можно назвать первой космической скоростью в атоме водорода.
Выражение для центрической постоянной (ЦП) можно использовать и при описании
свойств микромира, например, ЦП атома водорода равна 
, (8), где с – скорость света, 
– классический радиус электрона.
Постоянная Планка своим существованием обязана центрической постоянной (8) и квантованности микромира (о возможности существования траекторий не лежащих в диаметральной плоскости тел см. [1]).
Из (8) получаем значение постоянной тонкой структуры 
, (9).
С учетом изложенного выше, найдем соотношение для элементарного
заряда. Для этого воспользуемся формулой постоянной тонкой структуры из
квантовой электродинамики
,
(10)
где 
– магнитная постоянная.
Подставляя в (10) значения h и 
из (7) и (9), получаем выражение для заряда электрона
,
(11)
а учитывая (8) – другой вариант этой формулы
,
(12)
Что может означать физический смысл полученного выражения? В квантовой
теории считается, что в результате нулевых колебаний (флуктуаций) вакуума
непрерывно возникают и исчезают электрон–позитронные пары. Автор представляет
этот процесс, как динамическую симметрию вселенной [6], т. е. физический
мир существует, условно говоря, в виде двух взаимопроникающих неразделимых
вселенных: "положительной" и "отрицательной". Если,
опять же условно, считать нашу вселенную "положительной", то
рождение в ней электрона с массой
и объемом с радиусом
, соответствует рождению частицы в "отрицательной" вселенной,
в которой наша масса инвертируется в объём с радиусом ,
а наш объём радиусом
инвертируется в массу, численно равную .
Отсюда, величина 
означает линейный размер элемента вселенной, который мы называем зарядом.
Из формулы (11)
становится ясен физический смысл знака заряда: он определяется относительным
направлением скоростей
и с.
Нами получены соотношения (7), (9), (11) и (12), в которые входят только
фундаментальные константы, поэтому их можно использовать во всех известных
формулах физики для раскрытия физической сущности описываемых ими явлений.
Мы выяснили, что количественное соотношение для центрической постоянной
"работает" и в микромире. Воспользуемся его свойством (1) и
(2) для вычисления гравитационной постоянной электрона. Обозначим ее 
.
С учетом 
, (8) , отсюда
,
(13)
ее численное значение равно
,
которое больше астрономической
в
раз. (14)
Полученный результат означает,
что не является константой! Теперь выясним, от каких параметров зависит
ее величина. Для этого воспользуемся формулой (11) и законом Кулона следующим
образом.
Сила взаимодействия зарядов в вакууме равна 
,
где 
- электрическая постоянная, r – расстояние между зарядами. Раскроем
значение
и перепишем формулу снова
, (15)
В соотношении (11) тройка параметров (,
и )
являются константами из-за квантованности микромира. Предположим, что
они могут принимать любые другие значения. Тогда для произвольного тела
сферической формы мы можем написать
,
(16)
где V – скорость на первой g – поверхности тела (первая
космическая скорость), m – масса тела, R – радиус первой
g – поверхности. Подставляя (16) в (15), находим силу взаимодействия
двух тел
,
(17)
где индексы 1 и 2 означают номер соответствующего тела. Перегруппируем
члены так, чтобы выделить часть формулы, соответствующую традиционной
записи закона тяготения Ньютона
.
(18)
Из (18) получаем выражение для кавендишевой гравитационной "постоянной"
.
(19)
Теперь видно, от каких параметров зависит ее величина.
Перепишем (19) таким образом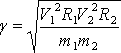 
.
Под корнем в числителе стоит произведение центрических постоянных, поэтому
мы можем написать
.
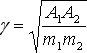(20)
Проверим (20) численно на системе Земля -Луна, используя справочные данные
.
С учетом (1) и (2) формула (20) преобразуется к виду
,
(21)
где 
и 
, соответственно, кавендишевы гравитационные постоянные первого и второго
тела. И так, каждому телу соответствует только своя гравитационная постоянная.
Для двух и более тел она отличается, главным образом из-за изменения плотности
тела (см. рис. 3).
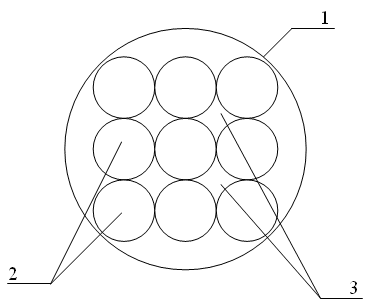
Рис. 3. Плотность ядра атома отличается от плотности составляющих его
нуклонов за счет появления промежутков между ними: 1 - граница ядра, 2
- нуклоны, 3 - промежутки между нуклонами.
Если распространить схему (рис. 3.) на атомы,
молекулы, тела и т.д., то становится понятно, почему гравитацонная постоянная
макрообьектов столь значительно
отличается от электронной
(см. 14). Наиболее точные определения кавендишевой гравитационной постоянной
в лабораториях мира показывают
недостаточную сходимость результатов (см. таблицу).
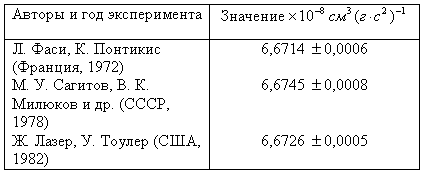Специалисты
относили это на погрешность экспериментов. Однако, согласно (19) расхождение
результатов действительно должно быть, если для измерений в экспериментах
использовались различные тела.
Что
касается современного значения ,
используемой в астрономических расчетах, то уверенно отличать вариации
ее величины пока еще не позволяет достигнутая точность экспериментов.
Соотношение (18) обнаруживает новое свойство гравитационного взаимодействия
объектов, которое отсутствует в известной формуле закона тяготения Ньютона:
в зависимости от знака скоростей
и сила
F тоже может иметь различный знак. Последний результат говорит
о том, что тела могут не только взаимно притягиваться, но при указанных
условиях взаимно отталкиваются.
Заключение
И так, с использованием законов классической физики выведены аналитические выражения для фундаментальных физических констант. Сделан вывод о непостоянстве кавендишевой гравитационной "постоянной" и возможности гравитационного взаимоотталкивания тел. Полученные в работе соотношения раскрывают физическую сущность явлений и эффектов, описываемых известными выражениями. Для уточнения и проверки полученньк результатов необходимы дальнейшие теоретические и экспериментальные исследования.
Литература
- Линевич Э. И. Явление антигравитации физических тел (ЯАФТ). – Хабаровск: ПКП "Март".1991. 20с. (Россия).
- Линевич Э. И. Геометрическое обоснование эксперимента Хаясака – Такеучи с вращающимися роторами.– Доклад на 2-ой СНГ Межнаучной конференции "Единая теория мира и ее практическое применение". 20 – 21 сентября 1993г., Петрозаводск. (Россия).
- Милюков В.К., Сагитов М. У. Гравитационцая постоянная в астрономии. – Космонавтика, астрономия. 1985. №.9. 64с. (Россия).
- Золотарев В. Ф., Шамшев Б. Б. Физика квантованного пространства – времени. Часть 1. Издательство Саратовского университета. 1992. 104с. (Россия).
- Золотарев В. Ф., Шамшев Б. Б. Физика квантованного пространства – времени. Часть 2. Издательство Ульяновского политехнического института. 1993. 100с. (Россия).
- Линевич Э. И. Динамическая симметрия вселенной. – Природа и аномальные явления. Владивосток. 1995. № 1 - 2, с.6. (Россия).
- Линевич Э. И. Гравиинерционный двигатель. Патент № 2080483.
- Черняев А. Ф. Инерция – движение взаимодействия. Москва. 1992. 84с. (Россия).
- Hayasaka H., Takeuchi S. Phys. Rev. Lett. 1989. V. 63. 25. P. 2201 – 2704.
- Kishkintsev V. A. The Eotvos Correction Applied to the Thermal Motion of Gas Molecules. Galilean Electrodynamics, V. 4. #3. 47 – 50. 1993.
- Forward, R. L. “Far Out Physics”, Analog Science Fiction/Sciense Fact, Vol 95. Aug. 1975. P. 147 – 166.
- Forward, R. L.
“Negative Matter Propulsion”, AIAA Paper 88 – 3168, July 1988.
Ноябрь 1999 г., Атём, Приморский край
