Современное
промышленное развитие цивилизации основывается на физике Ньютона-Эйнштейна,
а она по своей сути является математическим представлением природы: в
нём совершенно отсутствуют выводы, которые можно получить из образного
восприятия окружающего мира. Последнее означает способность мысленно превращаться
(погружаться) в физический процесс, ощущать все его тонкости, т. е. временно
становиться самим процессом. Это умение позволяет быстро находить ответы
даже там, где любая математика бессильна. Мы оценим некоторые положения
современной классической физики с точки зрения такого представления, так
как это имеет непосредственное отношение к нашей теме.
Первый закон Ньютона гласит: «Если на тело не
действует внешняя сила, то оно находится в состоянии покоя или равномерного
прямолинейного движения». Покажем пример несоответствия трактовки закона
опыту.
Под действием гравитации тела падают с ускорением.
Представим, что мы находимся в замкнутой кабине, которая, в свою очередь,
падает с ускорением свободного падения. Как читатель догадывается, все
тела в кабине будут находиться в состоянии относительного покоя или равномерного
прямолинейного движения ( все тела в кабине будут в состоянии невесомости
). Для чистоты примера, оговоримся, что в одномерном случае (как в нашем
примере) специальными экспериментами внутри кабины всё таки возможно обнаружить
ускоряется она или нет, потому что пространство гравитационно искривлено
(Черняев А. Ф. Инерция - движение взаимодействия. М.: 1992). Однако, для
многомерного (изотропного) ускорения состояние тел будет удовлетворять
букве первого закона, но не соответствовать физической сущности явления.
Ещё Р. Фейнман отмечал, «… что характерные, независимые
свойства сил не описал полностью ни Ньютон, ни кто-нибудь ещё…» (Фейнмановские
лекции по физике, вып. 1, стр. 209-210, «Мир», 1965). Мы говорим: «если
подействовать силой на тело, то оно ускоряется прямо пропорцио-нально
действующей силе и обратно пропорционально массе тела» (второй закон Ньютона).
На самом деле первоисточником силы является фундаментальное
свой-ство вещества (массы) и пространства сопротивляться (противодействовать)
любому ускорению. Это противодействие мы назы-ваем силой инерции. Другими
словами, мы хотим сказать, что если бы в природе отсутствовала сила инерции,
то отсутствовала бы и действующая сила: ускорение тела является первопричиной
появления силы инерции, на преодоление которой приходится создавать равнодействующую
силу.
Само существование сил инерции, по нашему мнению,
обязано изотропному расширению Вселенной (не зависимо от того, с ускорением
происходит этот процесс или с постоянной скоростью): ускорять тело, означает
противодействовать изотропному расширению в выделенном направлении. Пространство
и вещество образуют единую физическую систему: любое изменение состояния
вещества приводит к изменению состояния пространства и наоборот. Принадлежность
сил инерции к ускоряемому телу лишь кажущаяся: на самом деле силу инерции
создаёт пространство, которое занимает ускоряемое тело.
Первый постулат теории относительности Эйнштейна
гласит: «В любых инерциальных системах отсчёта все физические явления
протекают одинаково при одних и тех же условиях». Мы считаем, что этот
постулат и его количественные интерпретации основываются на наблюдении
любого физического явления изнутри процесса. Попробуем наше утверждение
пояснить как можно нагляднее.
Допустим, что начальник, распекая нерадивого сотрудника,
в порыве гне-ва стукнул кулаком по столу. С точки зрения относительности,
течение процесса и его последствия (имеем ввиду физику, а не кадровые
перестановки) не изменятся, если по неподвижному кулаку начальника с такой
же силой ударил стол. Однако, начальник, отождествляющий собой один из
двух инерциальных объектов (другой объект - стол), будет утверждать, что
это он стукнул стол, а не наоборот. Дело в том, что в нашем примере он
был не только участником физического процесса, но и одновременно наблюдал
процесс изнутри (поэтому имел возможность оценить реальность происходящего).
Третий участник разборки в лице горе-подчиненного, отождествляет собой
абсолютно неподвижную систему координат: он одновременно видел оба взаимодействующих
объекта со стороны (извне). Однако, он тоже будет утверждать, что не стол
ударил по кулаку, а наоборот. В данном случае оба будут правы, потому
что че-ловеческий мозг так устроен, что мыслит не уравнениями Ньютона-Эйнштейна,
а образно. В нашей голове окружающий мир отражается в ви-де реальных объектов
и процессов между ними, а на их основе мы и строим свои ответные действия.
Для создателей различных теорий не-подъёмной задачей является поиск абсолютной
системы координат, тогда как мысленно, мы можем легко представлять себя
в роли наблюдателя любого процесса со стороны (извне): тем самым, мы,
даже не догадываясь об этом, умеем превращать себя в абсолютно неподвижную
систему отсчета.
Теперь рассмотрим относительное взаимодействие
двух тел с формальной точки зрения. На рис.1 изображено тело 1, обладающее
импульсом p и неподвижное тело 2. 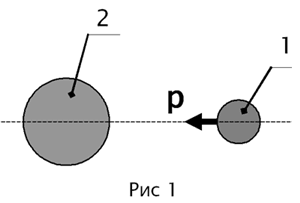 Пусть
первый наблюдатель находит-ся на теле 2. Вторым наблюдателем предлагаем
стать вам, уважаемый читатель. В некоторый момент времени тело 1 неупруго
сталкивается с телом 2. В момент начала взаимодействия система тел 1 и
2 имеет центр масс (цм) в точке 3. Мысленно закрепим начало абсолютно
неподвижной системы координат с этой точкой (см. Рис. 2). Результат взаимодействия
будет следующим. Первый наблюдатель увидит, как тело 1, приблизив-шись
столкнулось с телом 2 и нанесло ему и себе некоторые повреждения. Второй
наблюдатель увидит, что оба тела после взаимо-действия движутся со скоростью
V2 по направлению вектора импульса p, как показано на рис. 3. Теперь представим,
что первый наблюдатель на-ходится на теле 1 и повторим
Пусть
первый наблюдатель находит-ся на теле 2. Вторым наблюдателем предлагаем
стать вам, уважаемый читатель. В некоторый момент времени тело 1 неупруго
сталкивается с телом 2. В момент начала взаимодействия система тел 1 и
2 имеет центр масс (цм) в точке 3. Мысленно закрепим начало абсолютно
неподвижной системы координат с этой точкой (см. Рис. 2). Результат взаимодействия
будет следующим. Первый наблюдатель увидит, как тело 1, приблизив-шись
столкнулось с телом 2 и нанесло ему и себе некоторые повреждения. Второй
наблюдатель увидит, что оба тела после взаимо-действия движутся со скоростью
V2 по направлению вектора импульса p, как показано на рис. 3. Теперь представим,
что первый наблюдатель на-ходится на теле 1 и повторим 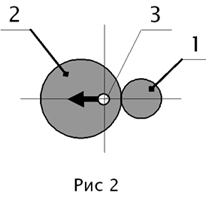 тот
же эксперимент. Результат взаимодействия тел будет следующим. Первый наблюдатель
увидит, как тело 2 приблизившись, столкнулось с телом 1 и нанесло ему
и себе такие же повреждения, как и в первом эксперименте. Второй наблюдатель
уви-дит, что оба тела после взаимодействия движутся, как и в первом эксперименте
со скоростью V2 по направлению вектора импульса p, как показано на рис.
3.
тот
же эксперимент. Результат взаимодействия тел будет следующим. Первый наблюдатель
увидит, как тело 2 приблизившись, столкнулось с телом 1 и нанесло ему
и себе такие же повреждения, как и в первом эксперименте. Второй наблюдатель
уви-дит, что оба тела после взаимодействия движутся, как и в первом эксперименте
со скоростью V2 по направлению вектора импульса p, как показано на рис.
3.
Мы так подробно описали простейший эксперимент
по взаимодействию двух тел для того, чтобы показать, что относительность
взаимодействия - кажущаяся. Причина его кроется в наблюдении физического
процесса из-нутри этого процесса. Повторим ещё раз: согласно теории относительности
в разных инерциальных системах один и тот же процесс протекает одинаково,
т. е. - динамически симметрично. 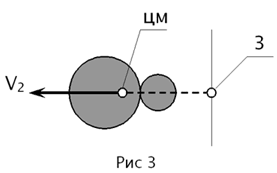 Однако,
наш эксперимент показывает, что при наблюдении его в абсолютно непод-вижной
системе координат, мы обнаруживаем, что этот же процесс может иметь только
одно направление во времени и пространстве т. е. он динамически несимметричен.
Однако,
наш эксперимент показывает, что при наблюдении его в абсолютно непод-вижной
системе координат, мы обнаруживаем, что этот же процесс может иметь только
одно направление во времени и пространстве т. е. он динамически несимметричен.
Этот вывод, в том числе, показывает границу применимости
теории от-носительности. В частности, она непригодна для описания безопорного
взаимодействия. Для этого случая, как ни покажется странным, годится второй
закон Ньютона. А всё потому, что, как уже говорилось, он на са-мом деле
даёт количественное описание взаимодействия вещества (массы) с пространством!
Таким образом, можно обобщить, что любое изменение
состояния механической системы с использованием ускорения является абсолютным.
Его результат всегда однозначен во времени и пространстве.
Земная цивилизация на данный момент освоила только
опорный (реактивный) вид взаимодействия тел. В таком способе взаимодействия,
если учесть все взаимодействующие объекты (включая земной шар, солнечную
систему и т. д.), мы обнаружим, что центр масс системы ни куда и нико-гда
не перемещается: всегда остаётся неподвижным. Отсюда, известный закон
сохранения импульса системы тел на самом деле повсеместно применяется
для описания псевдоизолированных систем, поэтому абсолютные безапеляционные
ссылки на него неправомерны: существует исключение из правил.
Никто не отрицает, что если часть механической
системы приобретает импульс за счёт изменения импульса остальной части,
то в результате центр масс системы остается неподвижным. Но возможен случай,
когда часть системы может приобрести импульс за счёт её внутренней энергии,
но без изменения импульса остальной части системы. После этого можно воздействовать
приобретённым импульсом на всю механическую систему и, тем самым, сдвинуть
в пространстве её центр масс. Такому преобразо-ванию можно даже дать условное
название, например, трансверсия.
На рис. 4 показана колебательная система, состоящая
из двух одинаковых дебалансов 1 и 2, которые под действием силового привода
3 могут вращательно колебаться каждый с 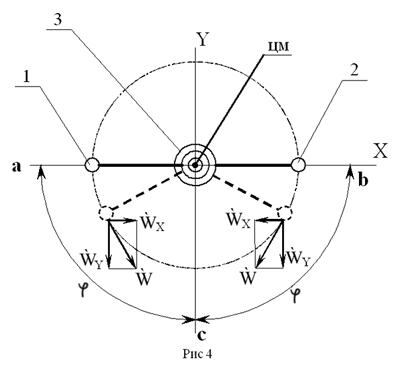 угловой
амплитудой
угловой
амплитудой ![]() . Процесс начинается
из исходного положения a и b с тангенциальным ускорением
. Процесс начинается
из исходного положения a и b с тангенциальным ускорением ![]() .
В точке с происходит реверс тангенциального ускорения
.
В точке с происходит реверс тангенциального ускорения ![]() (изменение его направления на противоположное). Мгновенное положение центра
масс всего устройства обозначено цм. Наблюдателя расположим в абсо-лютно
неподвижной системе координат, начало которой совпадает с цм.
(изменение его направления на противоположное). Мгновенное положение центра
масс всего устройства обозначено цм. Наблюдателя расположим в абсо-лютно
неподвижной системе координат, начало которой совпадает с цм.
Из рис. 4 видно, что в нашем случае мы имеем дело
с двумя линейными колебательными процессами (с двумя осцилляторами), наложенными
друг на друга во времени и пространстве. Первый осциллятор состоит, с
од-ной стороны из суммарной массы m дебалансов 1 и 2, с другой - всей
остальной массы М устройства (пусть её обозначает поз.3), колеблющихся
вдоль оси Y . Второй осциллятор образован двумя массами дебалансов 1 и
2 (каждая равна m/2), колеблющихся относительно друг друга вдоль оси X.
В нашем примере будем учитывать только радиальный момент инерции каждого
дебаланса. Их собственные моменты инерции принимаем равными нулю (технически
это сделать не сложно).
Непрерывный во времени колебательный процесс мысленно
разделим на отдельные фазы и будем исследовать их по порядку в старт-стопном
режиме. На рис. 5 показано положение тел в начале и в конце первой фа-зы
(поз. 4 обозначает центр масс двух дебалансов). 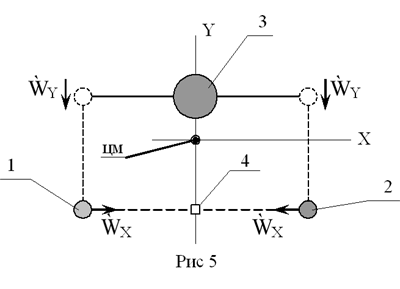 Мысленно
«заморозим» его и после этого начнём ускорять дебалансы 1, 2 относи-тельно
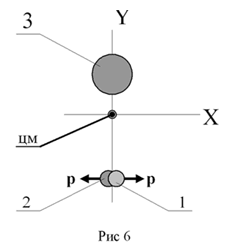
друг друга вдоль оси Х (перпендикулярно оси Y). Это будет началом второй
фазы. На рис. 6 показано расположение тел в конце второй фазы. Как видим,
в последнем случае каждый дебаланс приобрёл импульс p без изменения импульса
остальной массы системы. Это безус-ловно означает, что приобретенный каждым
дебалансом импульс является внешним по отношению ко всей механической
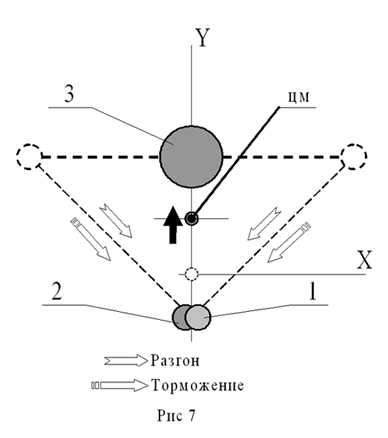
системе. На рис. 7 показан результат совмещения двух фаз движения в одной
схеме. В точке c происходит реверс тангенциального ускорения и одновременное
начало радиального поворота вектора > импульса p каждого дебаланса.
Как известно, ни радиальный поворот вектора, ни ускорение Кориолиса не
изменяют величину тангенциального импульса (Яблонский А. А. Курс тео-ретической
Мысленно
«заморозим» его и после этого начнём ускорять дебалансы 1, 2 относи-тельно
друг друга вдоль оси Х (перпендикулярно оси Y). Это будет началом второй
фазы. На рис. 6 показано расположение тел в конце второй фазы. Как видим,
в последнем случае каждый дебаланс приобрёл импульс p без изменения импульса
остальной массы системы. Это безус-ловно означает, что приобретенный каждым
дебалансом импульс является внешним по отношению ко всей механической
системе. На рис. 7 показан результат совмещения двух фаз движения в одной
схеме. В точке c происходит реверс тангенциального ускорения и одновременное
начало радиального поворота вектора > импульса p каждого дебаланса.
Как известно, ни радиальный поворот вектора, ни ускорение Кориолиса не
изменяют величину тангенциального импульса (Яблонский А. А. Курс тео-ретической
 механики.
Ч.2. Динамика. Изд. 4-е дополн., М., «Высшая школа», 1971). Отсюда, и
процесс торможения дебалансов 1 и 2, с воз-вратом их в исходное положение
относительно массы 3, в точности повторяется схемой на рис. 7. Фигурные
стрелки показывают направление действия сил, приложенных к дебалансам
со стороны привода 3.
механики.
Ч.2. Динамика. Изд. 4-е дополн., М., «Высшая школа», 1971). Отсюда, и
процесс торможения дебалансов 1 и 2, с воз-вратом их в исходное положение
относительно массы 3, в точности повторяется схемой на рис. 7. Фигурные
стрелки показывают направление действия сил, приложенных к дебалансам
со стороны привода 3.
И так, наш анализ работы колебательной системы
показал, что вдоль оси Y происходит процесс взаимодействия массы 3 с центром
масс 4 дебалансов 1 и 2. Это взаимодействие не меняет положение центра
масс цм всей системы, т. к. изменение импульса центра масс 4 дебалансов
1 и 2 происходит за счёт изменения импульса массы 3. Одновременно, каждый
из дебалансов 1 и 2, путём взаимодействия друг с другом пер-пендикулярно
оси Y, приобретает собственный импульс p, без изменения импульса массы
3, поэтому он является внешним по отношению ко всей механической системе.
Далее, в результате реверса тангенциального ускорения ![]()
 дебалансов
и радиального поворота векторов собственных импульсов p, происходит их
отдача на всю механическую систему. Тем самым, центр масс цм последней
начинает непрерывно с ускорением сдвигаться в пространстве в одну сторону,
а именно - в сторону действия силы инерции дебалансов. Работу по его перемещению
в пространстве производит само пространство, при этом линейная скорость
и кинетическая энергия системы непрерывно увеличиваются на протяжении
всего времени действия привода колебания. В работе (Линевич Э. И., Ежов
А. Ф. Инерционный движитель. «Новая энергетика» №3, 2004, с. 12-15) приведено
описание инерционного движителя принцип действия которого аналогичен вышеописанному
(более подробно см. WWW.dlinevitch.narod.ru). Его конструктивное отличие
заключается в том, что один из дебалансов заменён на гироскоп. Если использовать
в транс-портном устройстве только один движитель, то вследствие несимметричности
его привода возникает дополнительная поперечная вибрация. Однако этот
недостаток несущественен: во-первых, амплитуда вибрации весьма мала, потому
что эксцентриситет дебаланса из сообра-жений эффективности выбирается
порядка
дебалансов
и радиального поворота векторов собственных импульсов p, происходит их
отдача на всю механическую систему. Тем самым, центр масс цм последней
начинает непрерывно с ускорением сдвигаться в пространстве в одну сторону,
а именно - в сторону действия силы инерции дебалансов. Работу по его перемещению
в пространстве производит само пространство, при этом линейная скорость
и кинетическая энергия системы непрерывно увеличиваются на протяжении
всего времени действия привода колебания. В работе (Линевич Э. И., Ежов
А. Ф. Инерционный движитель. «Новая энергетика» №3, 2004, с. 12-15) приведено
описание инерционного движителя принцип действия которого аналогичен вышеописанному
(более подробно см. WWW.dlinevitch.narod.ru). Его конструктивное отличие
заключается в том, что один из дебалансов заменён на гироскоп. Если использовать
в транс-портном устройстве только один движитель, то вследствие несимметричности
его привода возникает дополнительная поперечная вибрация. Однако этот
недостаток несущественен: во-первых, амплитуда вибрации весьма мала, потому
что эксцентриситет дебаланса из сообра-жений эффективности выбирается
порядка ![]() 1мм, во-вторых, весь
привод устанавливается на стандартных амортизаторах. Главное его преимущество
заключается в следующем. Гироскоп очень жёстко удержи-вает в безопорном
пространстве плоскость инерции: чем быстрее мы будем пытаться поворачивать
её в поперечном направлении, тем сильнее гироскоп будет сопротивляться
(противодействовать) этому повороту. Такая схема движителя позволяет значительно
проще в безопорном пространстве управлять направлением тяги и её величиной.
Кроме того, противодействующий момент гироскопа прямо пропорционален скорости
поворота плоскости инерции (скорости его прецессии), а в схеме с двумя
дебалансами - пропорционален ускорению дебаланса.
1мм, во-вторых, весь
привод устанавливается на стандартных амортизаторах. Главное его преимущество
заключается в следующем. Гироскоп очень жёстко удержи-вает в безопорном
пространстве плоскость инерции: чем быстрее мы будем пытаться поворачивать
её в поперечном направлении, тем сильнее гироскоп будет сопротивляться
(противодействовать) этому повороту. Такая схема движителя позволяет значительно
проще в безопорном пространстве управлять направлением тяги и её величиной.
Кроме того, противодействующий момент гироскопа прямо пропорционален скорости
поворота плоскости инерции (скорости его прецессии), а в схеме с двумя
дебалансами - пропорционален ускорению дебаланса.
Линевич Э. И.
03 марта 2005г. (четверг)